俞龙-Data Player

这里我想针对两个点去继续讨论下。一、当我们的service level设置为95%的时候，这个95%具体指的是什么呢？ 二、库存的现货率和周转这两个主要的kpi的关系。 三、安全库存公式

一、当我们设置了95%的service level的安全库存的时候，可能从直观意义上，会认为就是我的订单满足率，可以达到95%。 根据wiki上的公式，我们也不难看出， 其实它主要针对的是vlt这段时间的销量的不确定性， 而这段时间的库存是随着时间一天一天消逝而慢慢减少，直至可能发生的缺货或者货物送达。 所以，其真正的意义是说vlt时间段内，有95%的时间段是可以满足所有订单的。 也就说，vlt时间段内，95%的时间段内，我的订单满足率应该是100%。

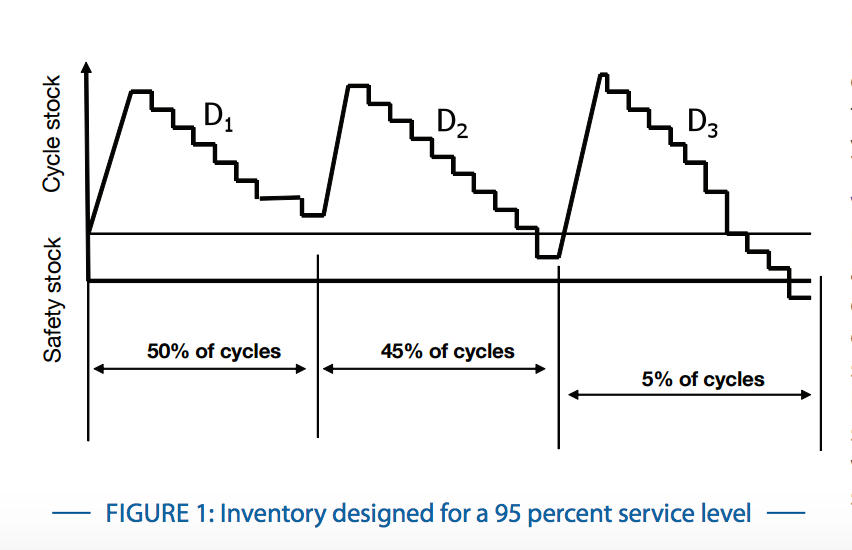
那么非vlt时间呢？也就是当前库存在补货点之上时候呢？当然是100%不缺货喽。 所以下个问题也就来了，当我们同时考虑vlt和非vlt时段的时候，情况发生了变化。 不妨先看个例子， 假设vlt是1周，供货商一次备10周的货，vlt时段的安全库存service level设置为50%，那么总体来讲， 它会有$\frac{9}{10}$的时间是非vlt时段，而$\frac{1}{10}$的时间是vlt时段， 而这段vlt时段会有50%的概率在这周发生缺货， 所以，假设2年100周，基本上会有$100\cdot \frac{1}{10} * \frac{1}{2} = 5$周左右发生缺货的情况。 也就是说95周都不会断货了，它与100周的比值为95%，假设称其为desired service level. 这样就延伸出来一个公式:

$$service\_level = 1- \frac{1- desired\_service\_level}{\frac{vlt}{order\_cycle}}$$

套用进去上面的例子：

$$50\% = 1- \frac{1- 95\%}{\frac{1}{10}}$$

这样总体的desired service level和我们vlt时间段设置的service level就对应起来了，而且我们惊奇的发现， 订购周期(order cycle)会十分影响service level， 假设我们想要总体的service level达到95%，那么即使不要safety stock，而只需要10倍于vlt的order cycle，也是可行的。

二、这里可以看出，当你的order cycle越长，那么现货率应该是越高的，然而，订购周期越长，也就意味着你要一次订购更多数量的商品。 同时也就意味着，你的周转会变慢，库存的持有成本会增加。 这里相信大家也可以看出来，现货这周转两个是存在制约关系的，我们在采购时候的，当以’少量多次’的形式采购，现货可能会下降，但是周转会变短。 而’多量少次’的形式则反之。与此同时，如果从成本的角度考虑的话，’少量多次’会增加订购成本， 而减少仓储持有成本， ‘多量少次’的则反之。那这种相互制约关系怎么去做取舍呢？答案就是最优化(optimization)。 库存管理很多模型都会基于最优化模型去求解, 这里就看你的目标函数怎么设计的了，比如在计算补货量的时候，如果你基于成本最优，那么可以得到很经典的EOQ模型。

三、 关于安全库存公式，我想提醒大家的是：

1 当我们在计算销量的方差的时候，$var(X) = E[(X-E(X))^2]$，我们的E(X)应该有是历史销量均值or预测值？还是都试试？

2 如果vlt是两周，但是销量预测只是预测一周总量，那么它们的标准差是否在同一水平？是否要做些转换呢？

3 如果你的不确定因素不仅仅只有vlt；或者vlt其实基本稳定了，不应该考虑它的不确定性，那公式还是这样么？

本文主要会聊一些关于库存管理(Inventory Management)的KPI,主要参考了Inventory Management Explained.

周转

周转有很多定义,其中我们最常用的应该是这一个样子:

sku的周转=sku的销量/sku的库存

从公式上我们可以看出来,它所反映的是sku的库存投入与销售量的比例。 这可能是最常用的反应库存指标的KPI,在Inventory Management Explained的作者看来, 这个KPI虽然很有用, 但可能是最为误用或者滥用的指标。 本质上, 这个KPI反应的仅仅是库存周转的速率,仅此而已, 并不是说高的周转就一定比低的周转好，不过很多误用的地方就在于此， 很多时候企业会以提高周转为主要目标。如果这样是我们所追求的， 那么采购的时候,直接将采购量降为一半、而采购次数变成2倍。 这一‘黄金准则’会使得我们的库存直接保持在原来的一半, 周转优化了整整两倍啊!可是,如果我们采购的成本很高,在财务上,我们这多出来一倍的采购成本是会导致亏钱的。 所以,再次重申,高的周转只意味着你的sku运转的更快了。 另外,Quora里面还有一个很有意思的讨论,它把成本维度的周转和毛利率 (Gross Margin or Gross Profit Percent ,GM%) 放在一起讨论。

GM%=$\frac{Sales−Cost}{Sales} =1−\frac{Cost}{Sales}$

如果周转考虑的不是销量角度的,而是成本角度的,那么公式如下:

InventoryTurns = $\frac{Cost}{AverageInventoryValue}$

通过上面两个公式,我们可以看到sku的周转可以转换成:

$$GM\% = 1 − \frac{InventoryTurns∗AverageInventoryValue}{Sales}$$ $$InventoryTurns = \frac{Sales(1−GM\%)}{AverageInventoryValue}$$

这里有个很有意思的联系:毛利率和周转是密切相关的,也就说,如果你知道了一个理想的毛利率,那么你也就可以得到一个理想的周转了。 （我不对此结论负责哈）

Gross Margin Return on Inventory Investment(GMROII)

Inventory Management Explained书中,作者给出了一个很俏皮的KPI–-GMROII. 它描述了你投入到库存的钱与商品的利润(毛利)的比率。 它反映了你每投入到库存的钱,如采购一定金额的商品,与这些库存内的商品获得的利润的比率。 这个指标很关键,因为它是直接反应你在库存是否很良好的转化为真金白银。 一个简单的例子(只计算毛利):如果你采购一个东东花了3块, 售价是10块,如果一年你卖了500件,这时总利润是7*500=3500. 如果这时平均库存数量维持在100件,那么投入到库存的钱是3*100=300块。 GMROII就是3500/300=11.67。 换句话说:你有300块钱,把他们都采购这件东东,并且一年的平均库存水平维持在100件, 然后一年你赚了3500块钱,回报率是11.67。 当然我们也可以通过净利润(net profit)计算,这样就可以看到哪些商品是最赚钱的,投资回报率最大的。 这样的KPI可以帮助我们做些什么呢? 或许我们可以先排序一下sku,看看哪些sku特别赚钱、投资回报率很高,那些投资回报率很低。 我们去分析看看有什么我们可以改进的地方去提升低回报率的sku,比如:提高售价。 有时候,某个sku的周转很高,看起来很赚钱,但是由于库存过多, 仓储成本过高,当你计算GMROII时可能不那么理想,并没有那么赚钱。

这些日子做库存管理感觉还蛮有意思的，之后的几篇blog我会介绍一些我对于库存管理一些概念的理解， 它们不一定是’正确’答案，不过却是我对于库存的一些认识。

说到库存管理，我觉得一句话足以描述：在合适的时间，以合适的形式(如持有、退货、补货等)， 对于sku（Stock Keeping Unit，简单理解为一件货品）进行操作，使得库存保持在合适的水平。 这句话随着我做事情的深入，便越来越觉得很精辟。 那么开始这段旅程吧，我们可以先来聊聊一个我觉得很意思的一个话题就是：安全库存(Safety Stock)。 相信有过库存管理经验的人一定对于这个概念不陌生，那么什么是安全库存呢？

安全库存顾名思义，就是防止断货的一种提前进行补货的策略。 试想，假设我们知道供应商送货需要10天，正常情况下，我们采取的策略是需要提前十天进行采购， 这样可以保证在可用库存为0的时候，我们新的订单就会到货了，这样就不会缺货拉。 然而，我怎么知道这十天会卖多少呢？最简单的方法就是使用历史的销量值，求得销量的期望。 再或者就做一些预测喽，然而，再准确的预测也不可能给出一个’正确的’答案。 理想情况下，销量预测和真实销量的差值(残差)会服从N(0,$\sigma$)的正态分布(Normal distribution)。 在这里插一句，关于Normal distribution这个钟形曲线， 在库存管理里面无处不在，由于它太’Normal’了，并且有着非常好的性质， 所以我们会有很多假设都是基于这个分布，后面我还会再次对于它进行讨论。 再回到刚才的话题，当我们根据销量预测的结果进行补货的时候，由于偏差，会有一半的概率导致缺货，一半的概率不会缺货。 举个例子，如果销量预测对未来一段时间预测是20件/天，一次补10天的货物， 那么当我们设置20*10 = 200件为我们的补货点的时候，如果10天的真实销量是180+或190+件还好，如果真实销量超过了200件， 那么断货就发生了。

那么很自然，我们就会想去进行提前补货以防止断货的发生。不过提前多久是合适的？1天,2天还是1周？ 这个就是引入安全库存的意义所在。 OK，那关于安全库存的本质，我觉得Inventory Management Explained这本书的观点描述的非常好。 ‘safety stock can be used to compensate for supply variablity. More specifically, we use it to compensate for the amount of demand variablity that may occur during the lead-time period.’

对于安全库存的意义,就是由于各个因素(如销量、vlt)的不确定性，使得我们要寻找一个缓冲， 可以容忍一定的变化范围，保证我们的库存减少断货的问题，同时又不要有过多冗余的库存。 关于这，我有个很认可的观点：我们不怕任何程度的变量，因为通过数学，尤其是统计的方法，我们可以量化出来这些变动。 在一些安全库存的公式中(如安全库存计算公式)， 会考虑销量预测的不确定性和vlt(vendor lead time–供应商送货时长)的不确定性，然而， 实际情况你可能还要量化如供应商能否有货的不确定性，销量预测的偏差等等，很难有一个公式能涵盖所有这些变化。 而一般来讲，vlt是影响最大的因素，所以一般的安全库存公式都只是考虑它，并不是说其他的不确定性就不应该考虑了。 至于安全库存计算公式，资料很多，大家可以参考wiki。 主要思路就是把各个因素的不确定性使用标准差表示并假设它们服从正态分布，这样通过正态分布的z-value（库存管理大都称其为称作’服务水平’）， 找到对应的一个值（如95%对应1.65），去计算相应的安全库存。 另外，这里附上安全库存公式的一个推导源自：

如果再给我一次机会(鄙人本科修数学)，我一定会学好一下三门课的。1 线代 2 最优化 3 概率统计 Why？

先说线代，如果说什么是最普遍的表现数据的话，那么大概也就是矩阵了，玩转线代也就是玩转矩阵，就这么简单。 现在满世界都在聊SVD，而一个最直接的例子就是PCA，这里我先介绍一篇blog，写的非常好的。可以看出来，数据降维的关键就是如何寻找新的坐标系去表示数据，也就是同样的数据，如何用更加少的维度去表示更加多的信息。 在寻找新的坐标系时，我们会用到协方差矩阵的对角化，eigenvector,eigenvalue等知识。在实施矩阵坐标变换，我们又会用到投影（projection）等知识。 似乎不会线代，就算知道了PCA整体流程，心里也总是隐隐不安。如果英文还不错，那么Introduction to Linear Algebra配合Gilbert Strang 老师的公开课一定是你的不二选择。 我相信就算大家以前学过这门课，也会再回头温习这们课的。

再说最优化，给我体会最深的是，最优化和神经元网络简直就是孪生兄弟，相信大家都有在SVM的对偶，kkt，拉格朗日搞来搞去的经历。 也会有思考梯度下降、牛顿法的过程。简单想想，从perceptron,MLP到SVM，都伴随着求解最小化损失函数的过程，相信这就是最优化的源头。我也一直怎么弄明白最优化，最近打算抱着Convex Optimization好好啃啃，再看看Stephen Boyd老师的公开课。

最后就是概率统计。很多时候统计学家就是在搞机器学习，很难讲就是哪个属于统计，哪个属于机器学习。不过给我做直观的一个区别就是，统计经常是对已有的数据进行分析，比如各个统计量，一阶、二阶矩等都是有其意义的，可以用来解释数据。而像置信区间，假设检验什么的也都是用“科学的”方法表现数据的意义。而机器学习更多是通过已有的数据训练，再应用到未知数据。当然，好消息就是像基于概率统计的贝叶斯分类器，我们可以通过它知道分类时，测试数据分到各个类别的概率是多少，这样的概率也给了我们去解释为什么的依据。

说了半天，其实我想说的时，这三门课在我看来是要伴随着对机器学习探索而不断重温的科目，各个算法都是基于前人不断迭代的过程，而数学就是这些的基石。

RandomForest在我印象里，是一个碉堡了的算法，因为用起来很简单，几乎不需要怎么调试就直接得到了很好地效果。 所以这也是为什么在Kaggle的Titanic分类竞赛专门拿RandomForest举例. 在学习RandomForest之前，请保证大家已经基本掌握了Decision Tree。这里有个很好的对于RandomForest的解释。

它的主要思想是将Decision Tree 聚合(ensemble)。根据wiki,它的实现主要 通过了bagging和Random subspace method两个方法。为什么要用这两个方法呢? Randomness! 前者是针对训练数据的随机选择，比如1000个实例中随机选择800个去生成树。 它的强悍之处在我看来是因为wiki里的这句话 “Increasing the number of trees tends to decrease the variance of the model, without increasing the bias.” Decision Tree的问题之一就是容易overfitting,显然bagging很好的解决了这个问题（更多关于overfitting请参考维数灾难到学习曲线)。 后者是针对feature去进行选择，比如从100个 features里面去选择50个,这使得每一个子树都不完全相同。之后再根据正常的Decision Trees算法去生成树，这里有个参数（free parameter）需要用户选择， 就是生成多少个trees，一般来讲，当然是越多越好了，最后根据各个trees的结果去投票(vote)，算出最终的结果。 但是tree多了以后运算会超级慢，这是个不得不要考虑进去的问题，准确+慢 vs 不准确+快？ 这时候，Out-of-bag error就是判定生成多大树的标准之一了，quora有个很好的解释， 大概就是说，在我们bagging的时候，从1000个实例选了800个，那么剩下的那200就组成了out-of-bag examples， 我们可以把这200个实例组成测试的trees，这样通过测试trees就可以大概知道RandomForest的精确度。

首先BIC是干什么的？用于比较在给定的数据下，比较不同模型的准则(criterion)。 怎么比较呢？他会关注两件事情，一更好的拟合结果，二更少的参数。一很好理解，二这是要求 一个相对更简单的模型去防止overfit这种事情。在想不起来的，请看这幅图。 既然是比较模型，那它也属于model selection的范畴了。 在wiki上写了好多感觉还蛮啰嗦的， 开始看了几遍也不怎么知道啥意思，其实主要的公式就是:(实例instance很多的情况下)

$$BIC = -2\cdot ln \hat{L}+k\cdot ln(n)$$

$\hat{L}$是已经完成了像MLE这种参数估计以后，得到的最优参数的似然函数(Likelihood function)。k是参数的个数，n是实例的个数。 一例胜千言，请大家直接翻到这个很棒的ppt，29页 有一个简单的例子，相信看完这个例子的人基本也就明白是怎么回事了。

这里有个很重要的叫做Likelihood function(似然函数)的概念，大家在Bayes rule里面应该也有看到过，然后在MLE(极大似然估计)里也有所耳闻。那么究竟它是怎么一回事呢？看个wiki的例子，非常形象~ 在硬币游戏里，H代表head，正常来讲，投掷时候得到head的概率为$P_{H}=0.5$，那么投掷两次都是head的概率是： $P(HH | P_{H}=0.5) = 0.25$。如果用likelihood function去描述它，那么就是: $L(P_{H}=0.5 | HH)=P(HH | P_{H}=0.5) = 0.25$, 它的含义并不是说给出了观察序列HH，我们得到概率$P_{H}=0.5$的概率是0.25。 相应地：$L(P_{H}=1 | HH)=P(HH | P_{H}=1) = 1$,它的含义也并不是说给出了观察序列HH，我们得到概率$P_{H}=1$的概率是1, likelihood function不是概率密度（probability density function），下面的图便是我们该问题里$P_{H}$的分布，可以看出 在观察序列都是HH的时候，我们更愿意相信$P_{H}=1$，这便完成了一次MLE的过程，在估计参数$P_{H}$的时候，我们更愿意相信 这个参数的取值是1。

另一方面，后验概率(Posterior probability)相对于likelihood function是一个逆过程。 如果是后验概率，这个问题就是$P(P_{H} | HH)$，其实没什么特别的，知道这个概念就好了， 看到Bayes Rule:

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

大家也就知道,后验概率是$P(A|B)$，似然函数是$P(B|A)$ ,先验概率是$P(A)$.

如果说以前的一些文章还有加入自己的思考的话，那这篇可能是最客观的表述。其实 Gaussian graphical model(GGM)资料还真的蛮少的，我本来也想找找书籍去学习下，结果到最后还是 要去看论文。当然，论文的力量就是可以把一个知识讲到令人发指的长，这篇blog主要是梳理GGM的主要脉络， 有兴趣的同学请直接参考相关论文文献。(Yuan and Lin, 2007 ; Friedman et al. 2008)

首先，什么是Gaussian graphical model？它围绕Gaussian分布的变量去研究各个变量的联系。具体来说就是 要研究Multivariate Normal Distribution.（插一句，这里Normal就是Gaussian，同义词，指正态分布，一般 我们会把很多变量假设为正态分布的，比较典型的就是回归问题里error项拉,其原因就是中心极限定理central limit theorem。） Multivariate Normal Distribution的核心，是inverse covariance matrix(ICM)，也叫concentraion matrix, precision matrix. ICM在Multivariate Normal Distribution的密度函数里面，他决定了Gaussian graphical model长什么样子哦。 好了，晕了的同学不好意思，必须要自己wiki一下Multivariate Normal Distribution， 尤其是一个重要的性质：设

covariance matrix: $\Sigma$ ,

inverse covariance matrix:C = $(\Sigma)^{-1} $

$C=(c_{ij})$

如果$c_{ij}=0$，那么变量i和变量j是独立的。也就是说，高斯图里，两个变量是没有联系的。 学过图论的都知道，图就是node和edge组成的，如果$c_{ij}=0$，则那两个nodes没有edge。 简单屡一下，高斯图模型重点是确定ICM长成什么样子，因为里面的元素为0代表相应的两个变量独立，也就确立了图的样子。 下面我们来聊一聊另一个我们追求的，就是’稀疏’（sparse）。什么意思呢？在图里，不是每一个连接（Edge）都是我们想要的， 换句话说，有时候nodes之间的edge有可能是噪音，应该被去除的， 而又有时候，你只想看哪些nodes之间的连接是显著相关的（significant）。所以这里有2个问题：其一，去除更多 不是很相关的连接，也就是让ICM里面有更多的0，即ICM更加sparse。方法？Lasso regularization。 其二，这是一个trade-off， 如果你想要保留更多的edges，lasso的惩罚项相应的就要小一点,保留的信息也就更多， 反之，你增大lasso的惩罚项，edges就少了，图也就更sparse了一些。

基于上述讨论，我直接给出我们要求解的表达式，具体过程请参考：(Yuan and Lin, 2007)

最大化：$log det (C) − tr(SC) − ρ||C||_{1}$

S is empirical covariance matrix.

解决上述最优化方程有很多方法，像Interior point methods等等，我在我的毕业设计采用了glsso(Friedman et al. 2008)。 它的优点就是快！他采用了block coordinate descent算法去求解上式，这个算法感觉就是奔着快去的。在这个链接里面的 Lecture 25有它的详细介绍，如果论文看不明白可以参考这个教程，其实我现在也在慢慢啃这个知识点，感觉还蛮难的，最优化没学好。。呜呜。。

Anyway,我的毕业设计是关于犬类疾病研究的，最后自己画了一匹藏獒和相应的gaussian graphical model.Link.

故事是这样的，在概率模型世界，我们要面对的问题就是这样的一个公式： $p(y|\bar{x})$, 其中，y是类别(class), $\bar{x}$是输入数据(input data)。 在Naive Bayes里面我们已经看到了如何用Bayes公式搞定这个问题。 这次，我们可以用个更直观的方式，怎么搞？ 这样？ $p(y|\bar{x})=w_{0}+\Sigma(w_{i} \cdot x_{i})$, 左边很熟悉（probabilistic model），右边也很熟悉(linear model)，但是，放在一起总是怪怪的。 计算机界有个名言，”Any problem in computer science can be solved by adding a layer of indirection” 这次，我们的’layer’就是logistic function。 没听过的同学请先看wiki的解释。 记住公式、记住图的样子，别问为啥。好了，再记住一个它的性质，1-$\theta(x) = \theta(-x)(\theta$表示logistic function)。对比图像看看，怎么样？很直观的一个性质吧。 logistic function就是把右边那个linear model的范围(无穷)缩小到probabilistic model的范围([0,1])了，从而可以让我们用概率的方法搞定它。

既然回归到了概率问题，那就用概率的方式解决。考虑一个普遍的binary classification问题：

它同样是bernoulli distribution。

引入logistic function, 将$w_{0}+\Sigma(w_{i} \cdot x_{i})$带入到logistic function得到： $\theta(\bar{w}\cdot \bar{x})= \theta(w_{0}+\Sigma(w_{i} \cdot x_{i}))=\frac{1}{1+exp(-(w_{0}+\Sigma(w_{i} \cdot x_{i})))}$

把它带入上面的方程，得到了: $P(y=+1|\bar{w}\cdot \bar{x})= \frac{1}{1+exp(-(w_{0}+\Sigma(w_{i} \cdot x_{i})))}$

和 $P(y=-1|\bar{w}\cdot \bar{x})=1-\frac{1}{1+exp(-(w_{0}+\Sigma(w_{i} \cdot x_{i})))}$

然后： $\frac{P(y=+1|\bar{w}\cdot \bar{x})}{P(y=-1|\bar{w}\cdot \bar{x})}= exp(w_{0}+\bar{w}\cdot \bar{x})$ (if > 1 , 正例)

两边取对数： $ln\frac{P(y=+1|\bar{w}\cdot \bar{x})}{P(y=-1|\bar{w}\cdot \bar{x})}=w_{0}+\bar{w}\cdot \bar{x}$

很神奇吧？线性分类器出现了！它的decision boundary就是$w_{0}+\bar{w}\cdot \bar{x}$, 这种神奇当然要归功于logistic function和它的性质喽！

然后呢，就是训练喽。这里用到的就是概率里面常用到的Maximum likelihood方法。一些推导我直接copy了，请注意 最后的那个就是目标函数。

问题又被转化为了最优化问题，它是convex的，有最优解，用Gradient Descent就完事了~这里不是课本，就是说这个思路拉。 再补一句，logistic regression会有过拟合问题，需要regularization。 经典方式又出现了: argmin(目标函数+regularization)

logistic regression在我看来是一个有很多标签的分类器。1 人们经常用它作为discriminative model的代表， 跟generative model的代表naive Bayes去比较(比如这篇)。 discriminative model & generative model请大家好好注意一下，这个 区别存在于很多其他地方哦。 (1)generative model是基于p(x,y), discriminative model是基于p(y|x),这样看来discriminative model更加直接， 对于直接的分类问题，准确性相对更高，而且p(x,y)会储存更多值 (2)generative model和discriminative可以互相转化，p(y|x)*p(x)就是p(x,y)。具体问题具体分析，有时候你可能要构建(x,y)而不是(x|y)。 2 它的名字虽然包含regression，但是它做的事情是classification。 3 它是个线性分类器。

上一篇简单聊了聊维数灾难， 这节就10只小猫小狗的例子稍微延伸一下，假设现在给你100只猫猫狗狗，3维已经不能满足线性可分了，这时候 可能直到10维我们才能找到一个超平面（hyperplane）去分离这100个小猫\小狗。但这时候，会引出这样一个问题，过拟合(over-fitting)。 也就是说，这时候尽管10维feature分离100个实例效果很棒，但是对于其他未知的小猫小狗(比如第101,102..个)，它的效果可能并不好！ 也就是说，训练数据(training data)的分类效果好并不等同于分类器在测试/未知数据(testing data)的效果好！ 我们所追求的应该是更少的泛化误差（generalization error）。

泛化的反面，就是记录（memorize）。10维的超平面在这里更像是记录我这100个动物是小猫或是小狗， 而不是学习(learning)。举个不恰当的例子： 还是之前的小猫\小狗，3维数据可以很好区分10个instances，假设到第11个小猫/小狗，3个feature可能不够用了，那么就增加到4个！ 然而这时你这第11个小猫小狗如果是noisy的，即误分类的，就也被‘记录’了下来，而每次发生feature不够用的情况，咱就增加一个feature， 最后就相当于你用了10个feature记录下了100个小动物是小猫还是小狗而已，即使这里面有误分类的，也给无情的记录下来了。 这种记录，对于其他待分类数据，是无用的。 这也就是为什么Decision Tree要选择‘最短路径’，Concept Learning要选择合取式(Conjunctive normal form)而不是析取。

(这里还要先请大家请自行google 一下cross-validation和bias/variance trade-off，因为后面的内容都是基于cross-validation的， bias/variance的概念也是要涉及到的。)

对于之前那样的过拟合问题，显然是一个high variance问题，这类问题我们的学习曲线(Learning Curve)大概是这样的：

相反地，一个high bias问题的Learning Curve：

对于分类问题，我们并不知道可以达到的最优结果(desired performance)是多少， 不过Learning Curve却是一个可以让你往这个方向去的直观的工具。 通过画Learning Curve，我们至少可以对现有的分类器有种‘感觉’，加之corss-validation，进而去避免high variance/high bias， 进而再通过优化自己的参数free parameter，去接近、达到desired performance。

本文原文摘自这里,作部分修改。

这篇文章，聊聊很普遍的一个机器学习现象Curse of Dimensionality。首先，维度怎么会是一种‘灾难’呢？通过下面这个 非常直观的例子，我们来看看。 现在有这么一个分类任务，就是要区分10只‘狗’or‘猫’，给定的特征(feature)是基于颜色的（红、绿、蓝）。现在呢，我们考虑第一个 feature——红色。

感觉不是太好？不能线性可分？那就再考虑一种feature——绿色！现在我们有2维feature了哦。

感觉还是不是太好？还是不能线性可分？那就再再考虑一种feature——蓝色！现在我们有3维feature了哦~

哇塞，现在可以找到一个平面去分离小猫小狗了！

这里要告诉大家一个事实，当维度越来越高的时候，那么线性可分的概率会越来越大，而且当其维度高到一定时候，线性可分的概率会到1。(源自Cover theorem)。 插播一下，我上面说的这个事实也是kernel trick的基础，所以本文跟kernel method有很大关系，他们的目的很简单，就是处理线性不可分数据，而处理的方法本质一样，而细节略有不同。 比如，来说RBF network可以使用Guassian function作为RBF function去处理线性不可分数据，SVM可能会选择kernel trick直接在高维度处理数据等等。 kernel method是机器学习很重要的一块，并不是说一定只能使用在SVM。我经常会觉得ML有时候更像是拼积木的游戏， 你想搭建一个城堡（SVM处理线性不可分数据），那你就会看看哪个积木（kernel trick）更适用，然后就拿过来用， 而积木(kernel trick)并不是说从属于你这所城堡。

回到直播，那么这时候我们会说：越高维度越好喽！ 很不幸，维度高的‘灾难’这是显现出来了。就我们这个例子来说，假设每个维度有5个单位间隔（unit intervals）， 开个玩笑的说：不太红，有点红，红，特别红，极度红。-_-! 那么10个instances的情况下，每个单位间隔有2个instance喽。 同样的问题升到2维，还是10个instances，但我们这时有5 x 5 = 25个单位间隔（unit squares）。 平均每个单位间隔这时只有 10/25 = 0.4个instance。 再升到3维就只有0.08了。 那这里的变化量就是我们的密度(Density), 也就是密度变得越来越小了，越来越稀疏(sparse)了。

下面这个图从另一个角度解释了维度高的‘灾难’。如果，分类器的feature的范围是0到1的连续情况，1维时候， 涵盖20%的feature只需要从全体（population）选20%个训练数据就可以了。但是如果升到2维， 我们确需要从全体选出45%的数据才能满足涵盖20%feature(0.45x0.45=0.2)。3维去要0.58(0.58^3=0.2)。 看来，相同的涵盖率，在维度增长时候，我们需要的训练数据是指数增加的。细细想想，也是很直观的， 更多的feature当然需要更多的训练数据喽，我在概率模型probabilistic Models (1) 也聊过关于训练数据多少的问题。

下面一节我还会继续这个话题，先休息一下~不过是另外一个角度，主要是说learning curve。