俞龙-Data Player

这篇的内容主要是摘自Machine Learning 这本书第一章节，我觉得蛮有收获的，希望可以提供一个不一样的角度。 另外，这本书真的不错，是我导师推荐的，最重要的是我们Sussex大学图书馆竟然有！我会告诉大家我们图书馆连一本介绍Ruby的书籍都没有么。。可能是因为这本书是Cambridge出的，作为英国同乡总要给些面子吧，就引进来了。

既然是‘俯瞰’，那肯定不是某些特定的技术。首先，问大家这样一个问题”Given a real world problem, how would you reduce it to a ml problem.(一个实际问题如何转化成一个ML问题？)” 引自reddit。 这样的问题好像很没有头绪，但是别慌。书里给出了一个蛮不错的答案：其实大多数机器学习问题都着重干的3件事是关于Task, Model, Feature的。 具体来说，实际的问题到底是要处理哪个Task：分类(classfication)? 回归(regression)? 聚类(clustering)? 而不同的问题也要根据其场景去选择不同的model（稍后详细描述）。 在真正使用模型的时候，更重要的可能是feature的选取、生成。例如：在SVM中的kernel trick就是一种关于feature的操作，亦或者 pre-processing。通常来讲，我们大多数情况下不能直接获取到适用于model的数据，自然要对feature进行一些处理喽。

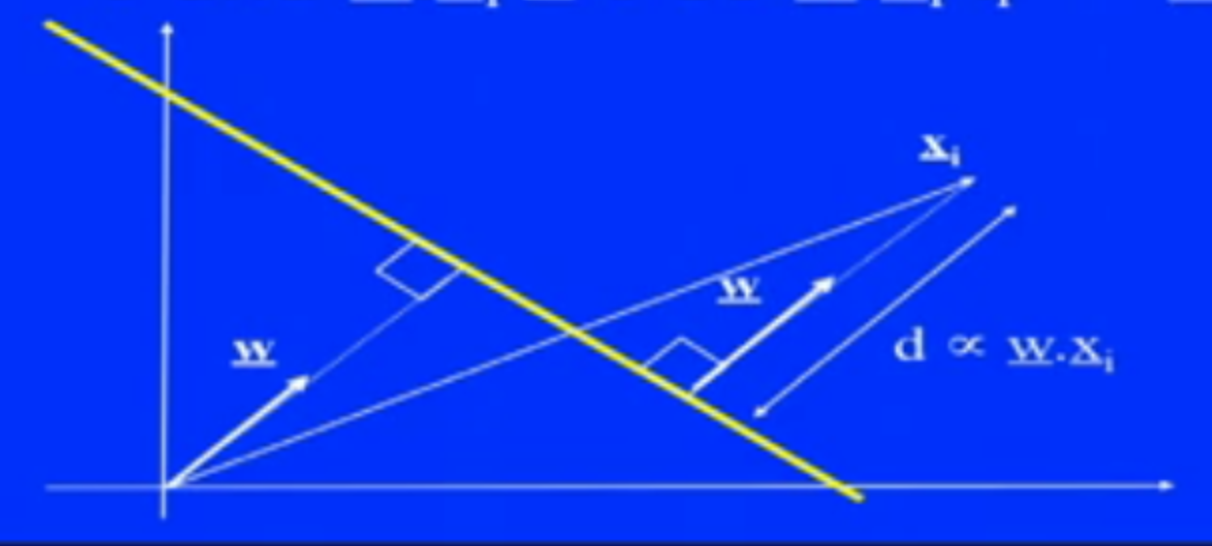
这里我重点想聊一聊Model。在作者看来，Model有三大类型：Logical model, Probabilistic model, Geometry model. 大家可以试着回顾一下3种model里面包含的算法。这里我分别举例一下他们典型的代表: Decision Tree, Naive Bayes, SVM。 这样分类有什么好处呢就是各个类别有其特点。比如 Logical model比较直观(主要是Tree的表现形式)，其很多思想源自computer science (如DNF,CNF)。 Probabilistic model的思想则更多是源自数学喽(尤其是概率与统计)。Geometry model也是很直观的，几乎所有课件都会来个二维平面， 然后各种正例反例加个decision boundary去解释来解释去，当然也免不了最优化，解析几何的一些数学概念。

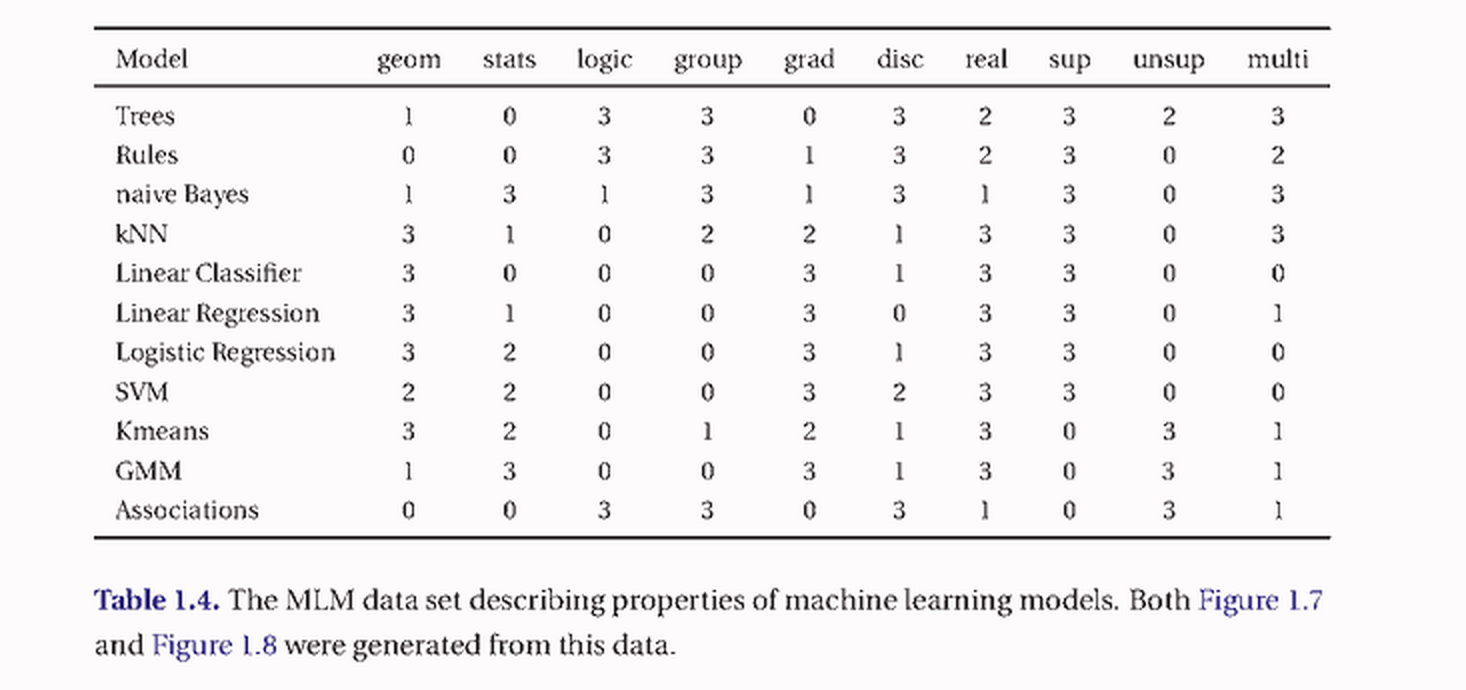
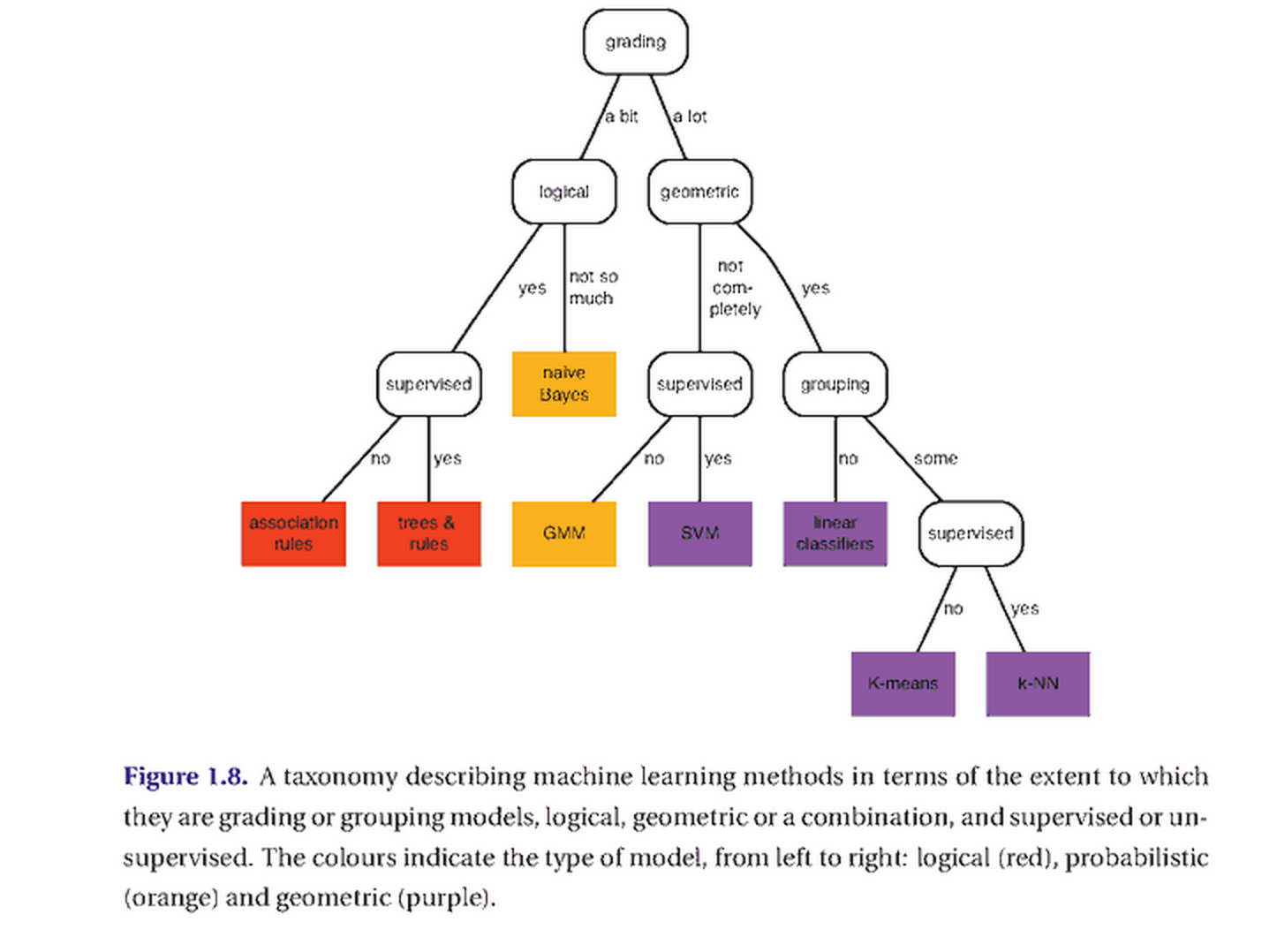
在处理实际问题时，不知道大家有没有在意过这样一个角度，这些模型其实还有个区别就是在于输入数据的类型，即离散值、连续值。 其对应的概念就是Grouping model, Grading model。举个例子：训练数据里面有两个正例为(5.0, 3.0), (1.3, 2.4)，两个个反例为(-5.0, -3.0), (-1.3, -2.4)。 对于Geometry model可能直接画个直线(decision boundary)，然后告诉你在直线的一侧，任何数据都是正例，另一侧都是反例(连续的感觉有木有)。 而对于Decision Tree,可能会问你这样的问题，对于新来的数据(x,y), x和y > 0乎?(离散的感觉有木有) 要是大于0呢，就是正例，否则呢，就都是反例。 从书里摘两个图给大家，希望大家能有个俯瞰的感觉。

字段说明(geometry model, probabilistic model, logical model, grouping model, grading model, discrete value, real value, supervised, unsupervised, multi-class)

感知器是相当重要的，原因很简单，它是Network的基础，不论是ANN，SVM，他们都有着类似基于感知器的神经元网络结构。 这也是为什么我在学校修Neural Network这门课时，光Perceptron的作业就占了50%的分数。 算法很简单，看看图很容易理解。 所以我在主要想聊聊这里面一些其他蛮有意思的东西， 在机器学习很多时候，我们发现”选择”是一个很重要的东西，不管是理论的建立还是实现的优化，都要做出种种选择， 今天我们就来看看Perceptron里面的一些选择题。

首先，想问下感知器的损失函数（loss function）的形式什么？ 在很多情况下，我们用到的损失函数形式都是这个样子的：(引用自Luc课件)

$E(\bar{w})=\frac{1}{2}\Sigma(t_{i}-y_{i})^2$ (1)

其中，$y_{i}$ 是感知器对于第i个实例(instance)的输出/预测(+1,-1)，$t_{i}$ 是第i个实例的原本的类别(+1,-1)。

为什么对于线性可分数据，普遍的感知器的loss function的选择却变成了这个样子？

$E(\bar{w})=-\Sigma \bar{w} \cdot \bar{x_{i}} \cdot t_{i}$ （for all misclassified $\bar{x_{i}}$） (2)

其中w是权重，$x_{i}$是第i个实例(instance)的值，$t_{i}$是第i个实例的类别。

由这个图，我们可以看到，(2)式可以告诉我们更多误分类(misclassified)点的信息， 具体来说，就是误分类点与分界线(decision boundary)的远近跟loss function成正比，这样loss function越大， 说明误分类点离得越远，反之亦然。 这样看来，(2)式就显得更加合理，因为每一次更新，如果某个误分类点的误差太大，那么这次更新的时候就纠正的更多。

至于更新法则：

$\bar{w}(t+1) = \bar{w}(t) + \eta \bar{x_{i}} \cdot t_{i}$ （for all misclassified $\bar{x_{i}}$）

(统计学习方法给出的形式)

等价于:

$$\bar{w}(t+1) = \bar{w}(t) + \eta \bar{x_{i}} \cdot (t_{i}-y_{i})$$

$y_{i}$感知器对于第i个实例的输出。(机器学习(Tom Mitchell)给出的形式)

另外的一个问题，对于我们这个问题，我们应该用批量(batch)梯度下降还是随机(stochastic)梯度下降呢？

简单的答案是随机(stochastic)梯度下降。(参考) 不过前提是数据线性可分，随机(stochastic)梯度下降的缺点之一就是会导致不能收敛，即使十分接近于极小值。

这一次我们做了几个选择题，而大家也可以看到， Perceptron的模型很简单，重点是要在适当的时刻选择一些适当的工具。 其实如果是现实的场景，面临的选择更多了，比如梯度下降的终止条件应该怎么选择？步长呢？初始值呢？ 如果数据线性不可分，我们的算法又要怎么选择？stochastic -> batch

之前说到我在公司是做Ruby on rails程序员，后来转到数据这块（小公司+好老板的好处就是可以无损的转去做自己喜欢的项目）， 面临的第一个项目就是做一个分类器，而我第一个采用的第一个模型就是概率模型(probabilistic models)， 具体分类器是朴素贝叶斯分类器。 效果在当时的我们看来，可以总结为三个字：碉堡了。我当时看到结果真的蛮震惊的，从前上课时候一扫而过的贝叶斯公式竟然有如此威力！

首先，如果对于朴素贝叶斯或者贝叶斯公式还不打了解的同学，我的建议是：拿出一张纸和一支笔，去阮一峰的blog 搜索、学习贝叶斯相关内容。（阮一峰的blog很有文采，强烈推荐之）。 在我看到‘朴素贝叶斯(Naive Bayes)’这几个字以后，对我来讲比较敏感的字眼其实是‘朴素(Naive)’两个字， 贝叶斯就贝叶斯，怎么还naive呢？ 其实，他表示的是一个简化的假设（assumption），即假设数据的特征(feature)/属性/字段是条件独立的(conditional independent)，why？ 举个例子（引用我的导师Novi）：假设我们要训练样例是20个features组成的，每个feature都是取值二元的（即可以取0或者1，no或者yes）， 样例的类别（class label）也是二元的，

$$p(X_{1},X_{2}..X_{20}|Y)$$

那么，概率的估计（probability estimates）有多少种可能呢？也就是假设空间(hypothesis space)的大小是多少？ 我的答案： $2^{21} -1=2097151个$ （每个Feature有两种，class label有两种，减1是因为概率之和必须为1，减去一个自由度）

所以这就导致了我们至少要学习2097151个样例才可以保证贝叶斯公式可以用，是不是很恐怖。 这也就是为什么我们需要一个条件独立假设，即

$$P(X_{1},X_{2}..X_{20}|Y) := P(X_{1}|Y)\cdot P(X_{2}|Y)...P(X_{20}|Y)$$

这时候，概率的估计（probability estimates）有多少种可能呢？ 我的答案是41个， （我的解释：对于每一项P(X|Y)来说，给定了Y值，X的自由度是1，因为其概率和是1，而Y有两种可能取值，所以一共2*20=40, 再加上P(Y)还有一个自由度，一共就是41） 显然，naive Bayes小了很多，对于训练的要求减小了。 那再引出一个问题，什么是‘不朴素(non-naive)’的分类器呢？

回归到我当时的任务，简单场景就是：每个商铺/网店都有一些描述信息，我们想根据字段的信息（比如‘地址address’）把他们分类到相关城市city去。 做这个任务的模型很简单，首先将地址分词，得到word1,word2,word3…,得到相应公式(以分成两个词为例)：

$$P(Y_{city}|X_{word1},X_{word2})=\frac{P(X_{word1}|Y_{city})\cdot P(X_{word2}|Y_{city})\cdot (p_{Y_{city}})}{P(X_{word1})\cdot P(X_{word2})}$$

由于分类时候，分子都是是一样的，可以不考虑。再假设 $P(Y_{city})$ 是均匀分布(uniform distribution)，又可以 忽略这个值（但不总是满足uniform distribution, 先验知识有时候是很重要的），那么最终的分类过程相当于

$$P^{\ast}(Y_{city}|X_{word1},X_{word2})=\operatorname{argmax}_Y (P(X_{word1}|Y_{city})\cdot P(X_{word2}|Y_{city}))$$

在实际应用时候，naive Bayes有个特别的优势：有些地址是不太好判别，而这一类的地址，在计算后验概率的时候， 概率较大的几组概率都很相近，导致很难‘确信’地把这些样例分类到相关城市。比如: (长春和北京都有朝阳区哦~)

$$P(Y_{北京}|X_{朝阳区})=0.3 , ~~ P(Y_{长春}|X_{朝阳区})=0.33$$

那么通过naive Bayes可以加一些简单的判断去提取这些很容易出错的实例，是不是很有用呢。^-^ 另外,先验知识(prior knowledge)也可以被当做因素考虑进来，例如：根据上面的概率 $P(Y_{长春}|X_{朝阳区}) > P(Y_{北京}|X_{朝阳区})$ 因此，这个实例应该被分到长春。

但是考虑先验知识 $P(Y_{北京})=0.5, ~~ P(Y_{长春})=0.3$

那么 $P(Y_{长春}|X_{朝阳区})\cdot P(Y_{长春}) < P(Y_{北京}|X_{朝阳区})\cdot P(Y_{北京})$ 因此，这个实例应该被分到北京。

‘hello world’似乎像是技术的入场礼，不同的人总在开始的时候用尽一些办法，就是为了看到’hello XXX’这几个字母 闪现在屏幕的那一刹那。现在我也盗用这个仪式，开始聊聊我对于Machine Learning(ML)的理解。 我觉得学东西直观的感觉(intuition)和基于问题的学习很重要啊，尤其是抽象的东西，比如: ML -_-! 所以我会主要通过这样方式谈谈我理解。同样，一些拼写标点错误也请大家见谅，从小考试都是丢三落四，所以老师 都给我起了个外号”准优等”。文笔我也不会很严谨，毕竟哀家才是研究僧，说话不会像公知一样对大家负责。 该啰嗦的就啰嗦到这里了~

总有一些事情是你一看上去就决定要终身相伴的，这可能就是我一看到machine learning的感觉吧。 还记得一年半前，我还是一个ruby on rails程序员，也是个应届生，在一家创业公司做码农。所以对于一切都是充满好奇，却也是很傻很天真。 总爱问别人很幼稚的问题，例如： 你为啥学这个啊？你觉得我学啥对我有帮助啊？等等这些。。 直到我发现一本书，集体智慧编程(Programming Collective Intelligence)，我觉得我的下一步应该是学这样子的知识！ 看起来很有用，而且也很高大上的样子。而且，恰好当时公司一个技术大牛也开始研究这个领域。我就抱大腿似的 准备跟他一起搞。后来，经过一阵小小研究后，我们竟然真的做成了一些项目，那会真是兴奋地不行不行的。后面会具体介绍。

其实我相信对于初学者，每个人都会觉得’我擦，这东西太难了吧！怎么需要学那么多东西。而且，它需要说得过去的数学功底。’ 是的，这是事实，毋庸置疑，要不岂不是谁都可以研究它了么。但是说白了，机器学习算法(algorithm)或者模型(model)本质来说就是一个 映射(mapping)而已，你所要的不就是将你的输入(input)得到个输出(output)么，而且那些复杂的算法往往开始的起因都是很简单的， 很多复杂的地方往往都是后期人们缝缝补补、增增减减的结果。这点，吴军老师在数学之美早有论述，我也对此坚信不疑，对了，这是一本好书。 但是，我在强调一下，但是，一些基础的先验知识很重要。已机器学习(Tom Mitchell)为例，概念学习那张我至少看了4遍， 还是没懂它在讲啥，什么归纳偏置(inductive bias)，假设空间，目标函数都不知道整这些概念干嘛使。 所以嘞，我的建议就是，弄了半天还不会的就搁一边，他会再出现的，到时候你肯定会如梦方醒的，因为慢慢积累这些概念以后， 会发现他们很多都是相通的，去弄懂某个孤立点的难度肯定比掌握点和点联系、区别困难很多。

最后我想说说我认为的学习机器学习的技巧吧。1 会读英文。不然，就只能看机器学习(Tom Mitchell)了吧。 可能也有别的选择，但我去年去清华蹭课他们用的就是这个教材，要是不靠老师讲解而是自学，蛮难的。 有些人很容易有个误会，就是会英文这门槛太高了，其实啊，专业词语就那么多，而且读英文的难度远远小于说和写， 开始慢慢来，之后就会很舒服了。2 直观理解。很多公式用一个图就解释的明明白白的。3 结合实践。看了不一定会明白， 明白了不一定理解，理解了不一定会做，做的话可以去(Kaggle.com)练练手。4 讲给别人。 我曾经问过我导师，我什么时候才能像你一样对于ML侃侃而谈，他笑着对我说:”等你可以把他讲给别人，让别人也理解，对于 他们的问题你可以解答。”这，就是为什么我开始写这个博客吧，而且，这是捷径。 5 基础知识,尽管数学面积很大，但至少梯度下降，贝叶斯这些必备知识要完全掌握。

一直说要搞个blog写写东西，结果拖拖拉拉一直到现在，很早之前读暗时间的时候就想搭建一个blog去总结一下知识，如今终于开始这个旅程了。我分享的东西也主要是自己的总结，如果偶尔有些话能帮助到各位看官我也就心满意足了。

我相信只有经过思考的知识才是有价值的，所以我的文字肯定都是自己经过思考去码的，大家如果有什么想法意见也希望思考后再传达给我。最终目标希望大家把这里视作一个平台，能让大家在这里汲取、思考。

为什么选择bboxers.com的域名？ 因为我喜欢节奏，尤其是bbox，我的偶像是alem。peace