俞龙-Data Player

首先BIC是干什么的？用于比较在给定的数据下，比较不同模型的准则(criterion)。 怎么比较呢？他会关注两件事情，一更好的拟合结果，二更少的参数。一很好理解，二这是要求 一个相对更简单的模型去防止overfit这种事情。在想不起来的，请看这幅图。 既然是比较模型，那它也属于model selection的范畴了。 在wiki上写了好多感觉还蛮啰嗦的， 开始看了几遍也不怎么知道啥意思，其实主要的公式就是:(实例instance很多的情况下)

$$BIC = -2\cdot ln \hat{L}+k\cdot ln(n)$$

$\hat{L}$是已经完成了像MLE这种参数估计以后，得到的最优参数的似然函数(Likelihood function)。k是参数的个数，n是实例的个数。 一例胜千言，请大家直接翻到这个很棒的ppt，29页 有一个简单的例子，相信看完这个例子的人基本也就明白是怎么回事了。

这里有个很重要的叫做Likelihood function(似然函数)的概念，大家在Bayes rule里面应该也有看到过，然后在MLE(极大似然估计)里也有所耳闻。那么究竟它是怎么一回事呢？看个wiki的例子，非常形象~ 在硬币游戏里，H代表head，正常来讲，投掷时候得到head的概率为$P_{H}=0.5$，那么投掷两次都是head的概率是： $P(HH | P_{H}=0.5) = 0.25$。如果用likelihood function去描述它，那么就是: $L(P_{H}=0.5 | HH)=P(HH | P_{H}=0.5) = 0.25$, 它的含义并不是说给出了观察序列HH，我们得到概率$P_{H}=0.5$的概率是0.25。 相应地：$L(P_{H}=1 | HH)=P(HH | P_{H}=1) = 1$,它的含义也并不是说给出了观察序列HH，我们得到概率$P_{H}=1$的概率是1, likelihood function不是概率密度（probability density function），下面的图便是我们该问题里$P_{H}$的分布，可以看出 在观察序列都是HH的时候，我们更愿意相信$P_{H}=1$，这便完成了一次MLE的过程，在估计参数$P_{H}$的时候，我们更愿意相信 这个参数的取值是1。

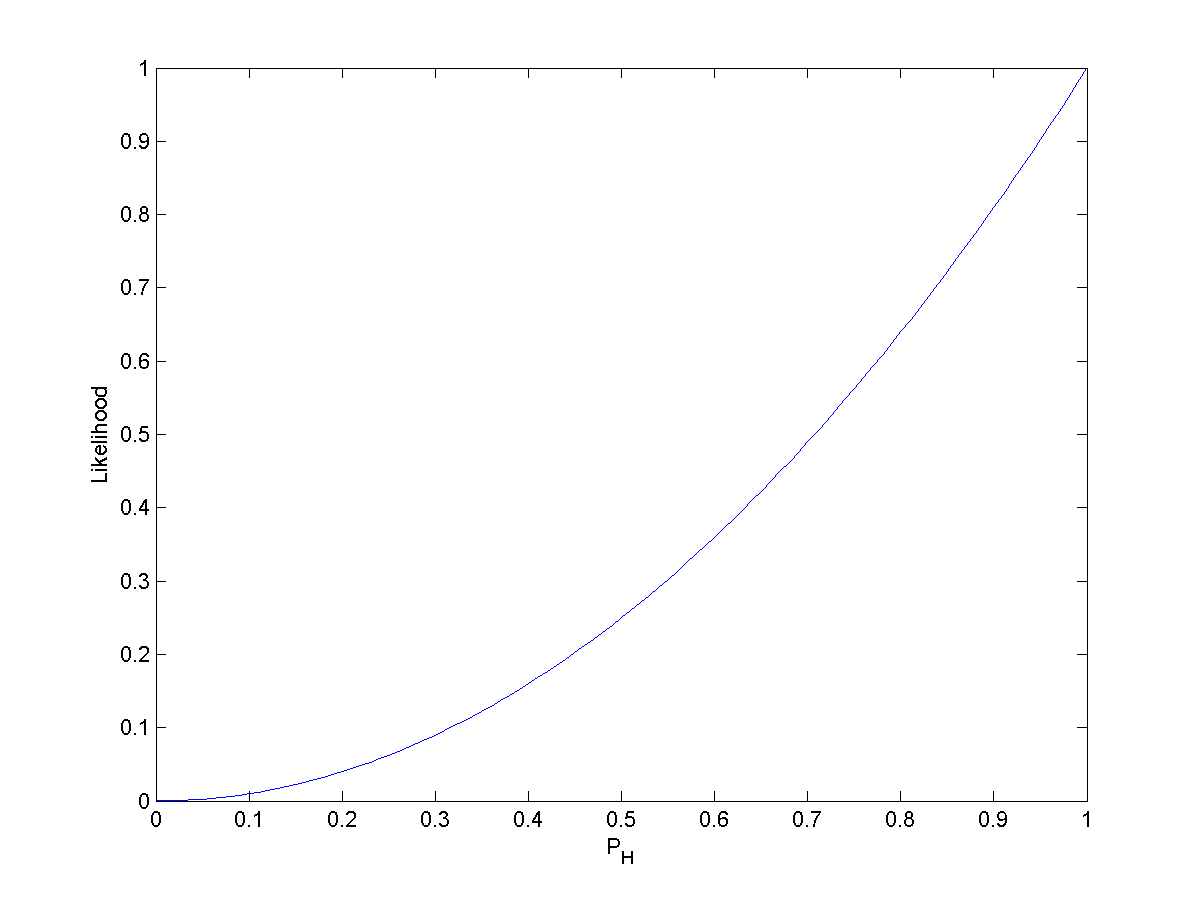
另一方面，后验概率(Posterior probability)相对于likelihood function是一个逆过程。 如果是后验概率，这个问题就是$P(P_{H} | HH)$，其实没什么特别的，知道这个概念就好了， 看到Bayes Rule:

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

大家也就知道,后验概率是$P(A|B)$，似然函数是$P(B|A)$ ,先验概率是$P(A)$.