俞龙-Data Player

故事是这样的，在概率模型世界，我们要面对的问题就是这样的一个公式： $p(y|\bar{x})$, 其中，y是类别(class), $\bar{x}$是输入数据(input data)。 在Naive Bayes里面我们已经看到了如何用Bayes公式搞定这个问题。 这次，我们可以用个更直观的方式，怎么搞？ 这样？ $p(y|\bar{x})=w_{0}+\Sigma(w_{i} \cdot x_{i})$, 左边很熟悉（probabilistic model），右边也很熟悉(linear model)，但是，放在一起总是怪怪的。 计算机界有个名言，”Any problem in computer science can be solved by adding a layer of indirection” 这次，我们的’layer’就是logistic function。 没听过的同学请先看wiki的解释。 记住公式、记住图的样子，别问为啥。好了，再记住一个它的性质，1-$\theta(x) = \theta(-x)(\theta$表示logistic function)。对比图像看看，怎么样？很直观的一个性质吧。 logistic function就是把右边那个linear model的范围(无穷)缩小到probabilistic model的范围([0,1])了，从而可以让我们用概率的方法搞定它。

既然回归到了概率问题，那就用概率的方式解决。考虑一个普遍的binary classification问题：

它同样是bernoulli distribution。

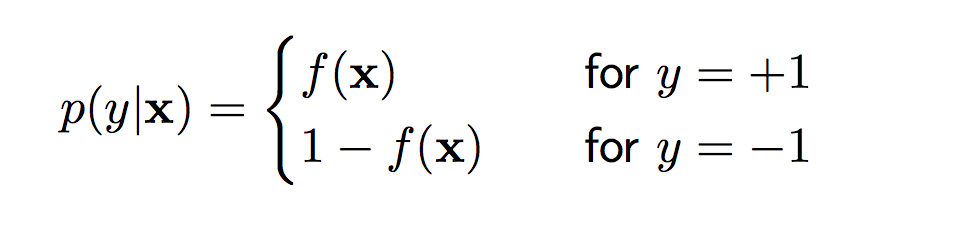
引入logistic function, 将$w_{0}+\Sigma(w_{i} \cdot x_{i})$带入到logistic function得到： $\theta(\bar{w}\cdot \bar{x})= \theta(w_{0}+\Sigma(w_{i} \cdot x_{i}))=\frac{1}{1+exp(-(w_{0}+\Sigma(w_{i} \cdot x_{i})))}$

把它带入上面的方程，得到了: $P(y=+1|\bar{w}\cdot \bar{x})= \frac{1}{1+exp(-(w_{0}+\Sigma(w_{i} \cdot x_{i})))}$

和 $P(y=-1|\bar{w}\cdot \bar{x})=1-\frac{1}{1+exp(-(w_{0}+\Sigma(w_{i} \cdot x_{i})))}$

然后： $\frac{P(y=+1|\bar{w}\cdot \bar{x})}{P(y=-1|\bar{w}\cdot \bar{x})}= exp(w_{0}+\bar{w}\cdot \bar{x})$ (if > 1 , 正例)

两边取对数： $ln\frac{P(y=+1|\bar{w}\cdot \bar{x})}{P(y=-1|\bar{w}\cdot \bar{x})}=w_{0}+\bar{w}\cdot \bar{x}$

很神奇吧？线性分类器出现了！它的decision boundary就是$w_{0}+\bar{w}\cdot \bar{x}$, 这种神奇当然要归功于logistic function和它的性质喽！

然后呢，就是训练喽。这里用到的就是概率里面常用到的Maximum likelihood方法。一些推导我直接copy了，请注意 最后的那个就是目标函数。

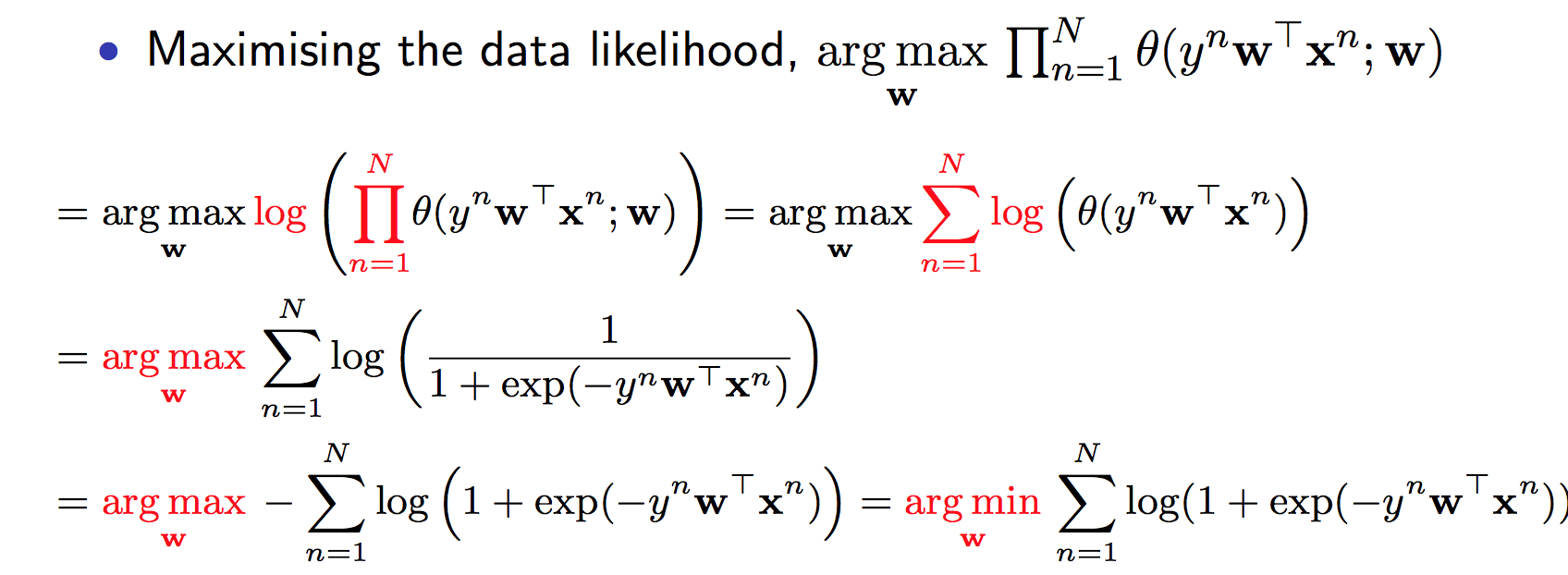
问题又被转化为了最优化问题，它是convex的，有最优解，用Gradient Descent就完事了~这里不是课本，就是说这个思路拉。 再补一句，logistic regression会有过拟合问题，需要regularization。 经典方式又出现了: argmin(目标函数+regularization)

logistic regression在我看来是一个有很多标签的分类器。1 人们经常用它作为discriminative model的代表， 跟generative model的代表naive Bayes去比较(比如这篇)。 discriminative model & generative model请大家好好注意一下，这个 区别存在于很多其他地方哦。 (1)generative model是基于p(x,y), discriminative model是基于p(y|x),这样看来discriminative model更加直接， 对于直接的分类问题，准确性相对更高，而且p(x,y)会储存更多值 (2)generative model和discriminative可以互相转化，p(y|x)*p(x)就是p(x,y)。具体问题具体分析，有时候你可能要构建(x,y)而不是(x|y)。 2 它的名字虽然包含regression，但是它做的事情是classification。 3 它是个线性分类器。