俞龙-Data Player

上一篇简单聊了聊维数灾难， 这节就10只小猫小狗的例子稍微延伸一下，假设现在给你100只猫猫狗狗，3维已经不能满足线性可分了，这时候 可能直到10维我们才能找到一个超平面（hyperplane）去分离这100个小猫\小狗。但这时候，会引出这样一个问题，过拟合(over-fitting)。 也就是说，这时候尽管10维feature分离100个实例效果很棒，但是对于其他未知的小猫小狗(比如第101,102..个)，它的效果可能并不好！ 也就是说，训练数据(training data)的分类效果好并不等同于分类器在测试/未知数据(testing data)的效果好！ 我们所追求的应该是更少的泛化误差（generalization error）。

泛化的反面，就是记录（memorize）。10维的超平面在这里更像是记录我这100个动物是小猫或是小狗， 而不是学习(learning)。举个不恰当的例子： 还是之前的小猫\小狗，3维数据可以很好区分10个instances，假设到第11个小猫/小狗，3个feature可能不够用了，那么就增加到4个！ 然而这时你这第11个小猫小狗如果是noisy的，即误分类的，就也被‘记录’了下来，而每次发生feature不够用的情况，咱就增加一个feature， 最后就相当于你用了10个feature记录下了100个小动物是小猫还是小狗而已，即使这里面有误分类的，也给无情的记录下来了。 这种记录，对于其他待分类数据，是无用的。 这也就是为什么Decision Tree要选择‘最短路径’，Concept Learning要选择合取式(Conjunctive normal form)而不是析取。

(这里还要先请大家请自行google 一下cross-validation和bias/variance trade-off，因为后面的内容都是基于cross-validation的， bias/variance的概念也是要涉及到的。)

对于之前那样的过拟合问题，显然是一个high variance问题，这类问题我们的学习曲线(Learning Curve)大概是这样的：

相反地，一个high bias问题的Learning Curve：

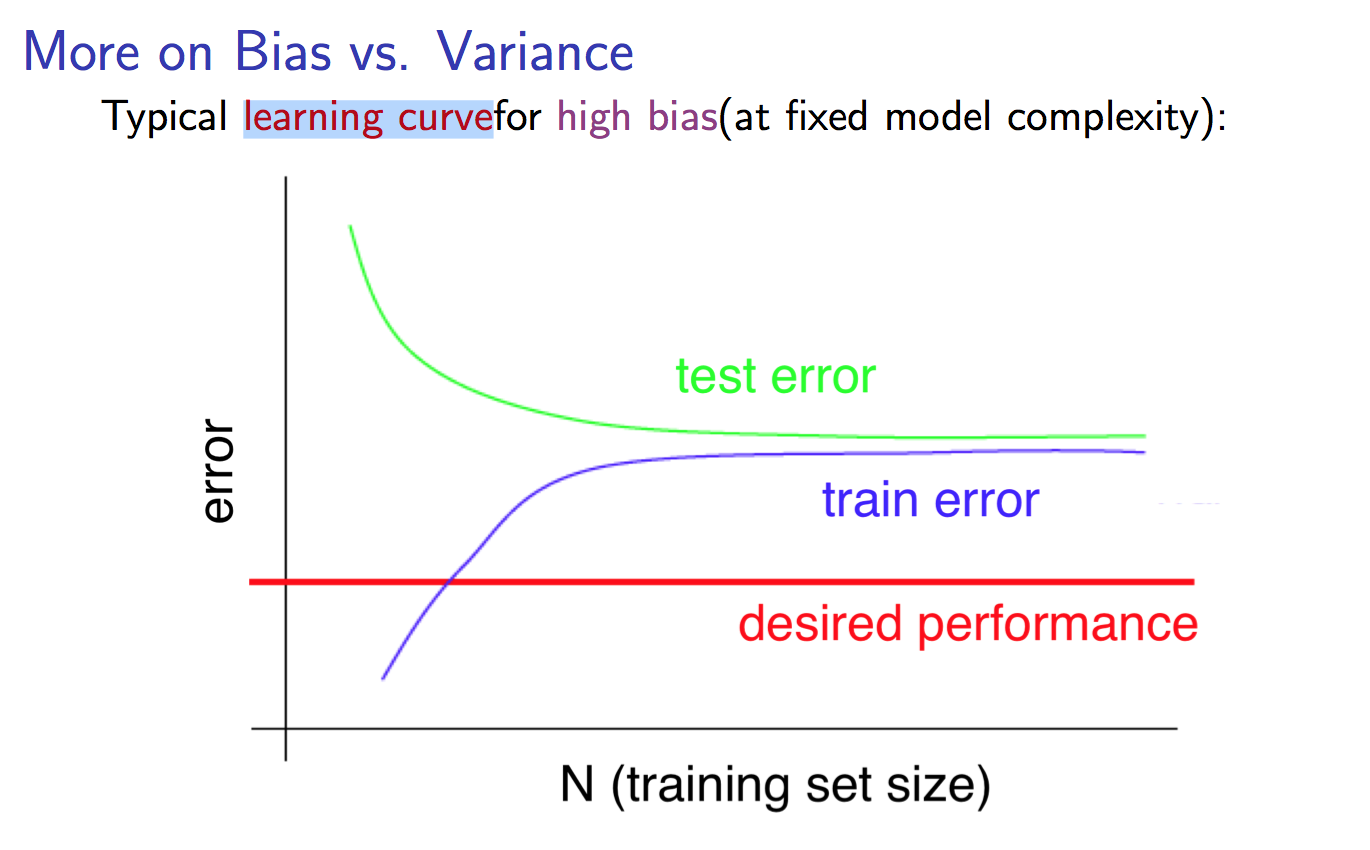
对于分类问题，我们并不知道可以达到的最优结果(desired performance)是多少， 不过Learning Curve却是一个可以让你往这个方向去的直观的工具。 通过画Learning Curve，我们至少可以对现有的分类器有种‘感觉’，加之corss-validation，进而去避免high variance/high bias， 进而再通过优化自己的参数free parameter，去接近、达到desired performance。