聊聊维数灾难(Curse of Dimensionality)
本文原文摘自这里,作部分修改。
这篇文章,聊聊很普遍的一个机器学习现象Curse of Dimensionality。首先,维度怎么会是一种‘灾难’呢?通过下面这个 非常直观的例子,我们来看看。 现在有这么一个分类任务,就是要区分10只‘狗’or‘猫’,给定的特征(feature)是基于颜色的(红、绿、蓝)。现在呢,我们考虑第一个 feature——红色。

感觉不是太好?不能线性可分?那就再考虑一种feature——绿色!现在我们有2维feature了哦。

感觉还是不是太好?还是不能线性可分?那就再再考虑一种feature——蓝色!现在我们有3维feature了哦~

哇塞,现在可以找到一个平面去分离小猫小狗了!
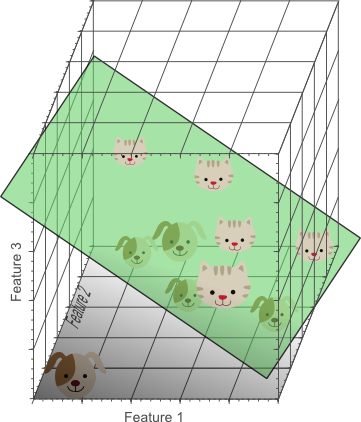
这里要告诉大家一个事实,当维度越来越高的时候,那么线性可分的概率会越来越大,而且当其维度高到一定时候,线性可分的概率会到1。(源自Cover theorem)。 插播一下,我上面说的这个事实也是kernel trick的基础,所以本文跟kernel method有很大关系,他们的目的很简单,就是处理线性不可分数据,而处理的方法本质一样,而细节略有不同。 比如,来说RBF network可以使用Guassian function作为RBF function去处理线性不可分数据,SVM可能会选择kernel trick直接在高维度处理数据等等。 kernel method是机器学习很重要的一块,并不是说一定只能使用在SVM。我经常会觉得ML有时候更像是拼积木的游戏, 你想搭建一个城堡(SVM处理线性不可分数据),那你就会看看哪个积木(kernel trick)更适用,然后就拿过来用, 而积木(kernel trick)并不是说从属于你这所城堡。
回到直播,那么这时候我们会说:越高维度越好喽! 很不幸,维度高的‘灾难’这是显现出来了。就我们这个例子来说,假设每个维度有5个单位间隔(unit intervals), 开个玩笑的说:不太红,有点红,红,特别红,极度红。-_-! 那么10个instances的情况下,每个单位间隔有2个instance喽。 同样的问题升到2维,还是10个instances,但我们这时有5 x 5 = 25个单位间隔(unit squares)。 平均每个单位间隔这时只有 10/25 = 0.4个instance。 再升到3维就只有0.08了。 那这里的变化量就是我们的密度(Density), 也就是密度变得越来越小了,越来越稀疏(sparse)了。
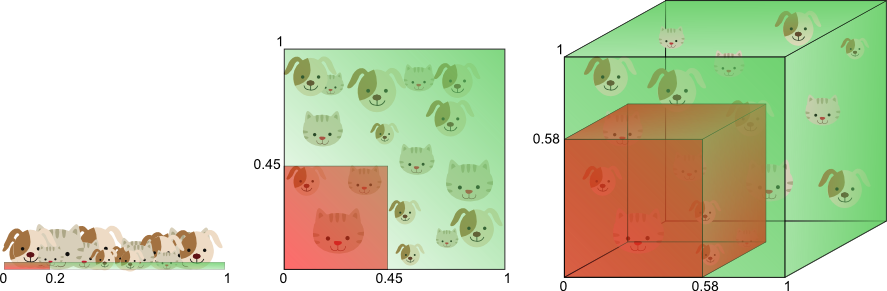
下面这个图从另一个角度解释了维度高的‘灾难’。如果,分类器的feature的范围是0到1的连续情况,1维时候, 涵盖20%的feature只需要从全体(population)选20%个训练数据就可以了。但是如果升到2维, 我们确需要从全体选出45%的数据才能满足涵盖20%feature(0.45x0.45=0.2)。3维去要0.58(0.58^3=0.2)。 看来,相同的涵盖率,在维度增长时候,我们需要的训练数据是指数增加的。细细想想,也是很直观的, 更多的feature当然需要更多的训练数据喽,我在概率模型probabilistic Models (1) 也聊过关于训练数据多少的问题。
下面一节我还会继续这个话题,先休息一下~不过是另外一个角度,主要是说learning curve。