感知器(Perceptron)里的选择题

感知器是相当重要的，原因很简单，它是Network的基础，不论是ANN，SVM，他们都有着类似基于感知器的神经元网络结构。这也是为什么我在学校修Neural Network这门课时，光Perceptron的作业就占了50%的分数。算法很简单，看看图很容易理解。所以我在主要想聊聊这里面一些其他蛮有意思的东西，在机器学习很多时候，我们发现”选择”是一个很重要的东西，不管是理论的建立还是实现的优化，都要做出种种选择，今天我们就来看看Perceptron里面的一些选择题。

首先，想问下感知器的损失函数（loss function）的形式什么？在很多情况下，我们用到的损失函数形式都是这个样子的：(引用自Luc课件)

$E(\bar{w})=\frac{1}{2}\Sigma(t_{i}-y_{i})^2$ (1)

其中， $y_{i}$ 是感知器对于第i个实例(instance)的输出/预测(+1,-1)，$t_{i}$ 是第i个实例的原本的类别(+1,-1)。

为什么对于线性可分数据，普遍的感知器的loss function的选择却变成了这个样子？

$E(\bar{w})=-\Sigma \bar{w} \cdot \bar{x_{i}} \cdot t_{i}$ （for all misclassified $\bar{x_{i}}$） (2)

其中w是权重， $x_{i}$ 是第i个实例(instance)的值，$t_{i}$是第i个实例的类别。

perceptron

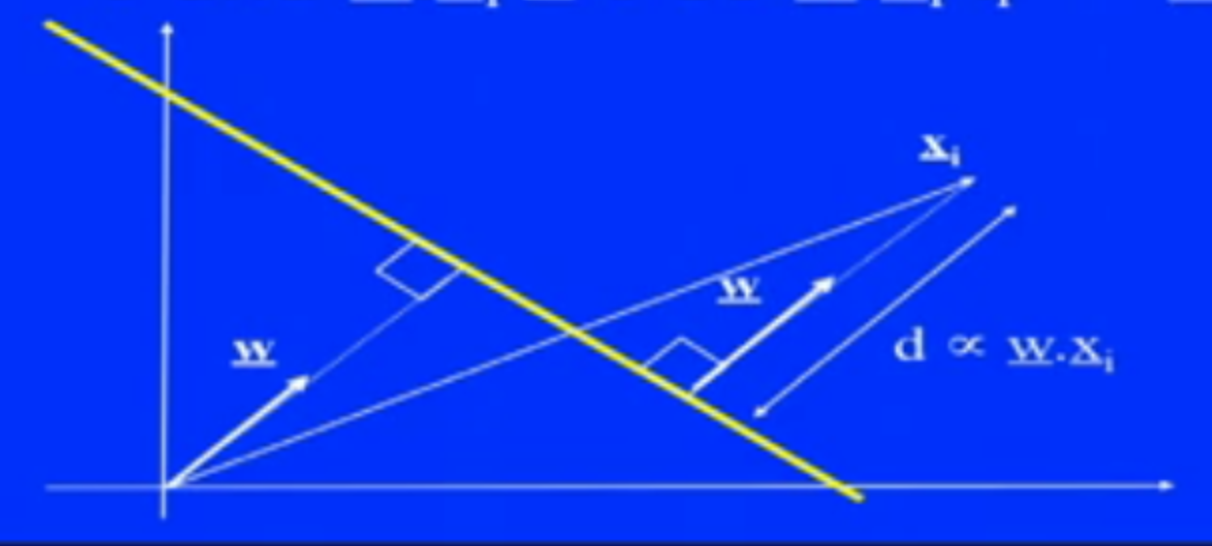
由这个图，我们可以看到，(2)式可以告诉我们更多误分类(misclassified)点的信息，具体来说，就是误分类点与分界线(decision boundary)的远近跟loss function成正比，这样loss function越大，说明误分类点离得越远，反之亦然。这样看来，(2)式就显得更加合理，因为每一次更新，如果某个误分类点的误差太大，那么这次更新的时候就纠正的更多。

至于更新法则：

$\bar{w}(t+1) = \bar{w}(t) + \eta \bar{x_{i}} \cdot t_{i}$ （for all misclassified $\bar{x_{i}}$）

(统计学习方法给出的形式)

等价于:

$\bar{w}(t+1) = \bar{w}(t) + \eta \bar{x_{i}} \cdot (t_{i}-y_{i})$

$y_{i}$感知器对于第i个实例的输出。(机器学习(Tom Mitchell)给出的形式)

另外的一个问题，对于我们这个问题，我们应该用批量(batch)梯度下降还是随机(stochastic)梯度下降呢？

简单的答案是随机(stochastic)梯度下降。(参考) 不过前提是数据线性可分，随机(stochastic)梯度下降的缺点之一就是会导致不能收敛，即使十分接近于极小值。

这一次我们做了几个选择题，而大家也可以看到， Perceptron的模型很简单，重点是要在适当的时刻选择一些适当的工具。其实如果是现实的场景，面临的选择更多了，比如梯度下降的终止条件应该怎么选择？步长呢？初始值呢？如果数据线性不可分，我们的算法又要怎么选择？stochastic -> batch